Tipos de vectores

¿Qué es un vector?

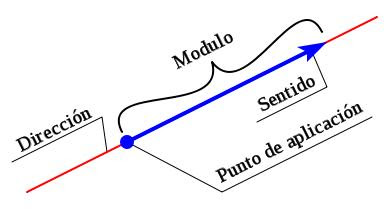
En física, el término vector se utiliza para mencionar a los segmentos orientados por medio de los que se representa, gráficamente, las magnitudes vectoriales. Cada vector debe contar, necesariamente, con los siguientes componentes: sentido, intensidad, punto de aplicación y dirección.

• El sentido es aquel que debe reflejar la orientación del vector. Para lograr esto, a la hora de graficarlo, se lo indica con la punta de la flecha de dicho vector.
• La dirección, en cambio, se lo representa a partir del ángulo que la línea del vector tiene en relación a otras rectas que funcionen como referencia.
• Por otro lado, la intensidad es la que logra reflejar cuál es la cantidad física del vector en cuestión a partir de una escala previamente establecida.
• Por último, el punto de aplicación es aquel punto en el que el vector actúa.

(El vector y sus componentes.)

Clasificación de los tipos de vectores

Los vectores pueden clasificarse de la siguiente manera:

Equipolentes: dentro de esta clasificación se considera a aquellos pares de vectores que tienen el mismo módulo, sentido y dirección.

Libres: se denomina como libres a aquellos vectores que conforman un conjunto de equipolentes. Esto quiere decir que son un conjunto de vectores que poseen la misma dirección, módulo así como también sentido.

Fijos: vectores como estos son los que poseen un origen que resulta fijo. Por medio de estas representaciones gráficas se logra representar una determinada fuerza en el espacio, o bien, qué posición posee un cuerpo.

Opuestos: los módulos de este tipo son los que si bien tienen la misma dirección y módulo, su sentido es opuesto, de allí su nombre.

Paralelos: en este caso, al menos dos vectores se ubican en rectas que resultan paralelas entre sí, de allí su nombre.

Deslizantes: bajo este nombre se identifica a todos los tipos de vectores que tienen la facultad de ir modificando su dirección a lo largo del trayecto de su directriz.

Ligados: bajo este nombre se menciona a aquellos vectores que, siendo equipolentes, se ubican en la misma recta. Esto implica que los vectores ligados comparten, además de la recta, el sentido, el módulo e incluso la dirección.

Concurrentes: los módulos como estos consisten en dos o más magnitudes vectoriales que poseen el mismo punto de origen.

Coplanares: los vectores conocidos bajo este nombre son aquellos que actúan en rectas que se encuentran en planos que son iguales entre sí.

Linealmente independientes: existen vectores como este cuando un conjunto de ellos carecen de una combinación lineal con el resto de los vectores. Esto implica que sean linealmente independientes

Linealmente dependientes: en este caso, una serie de módulos que si bien son independientes en lo lineal, su combinación lineal es equivalente al vector cero. Esto no significa que los coeficientes de la combinación lineal resulten iguales a cero.

Ortogonales: en este caso, un par de vectores deben tener un producto escalar equivalente a cero.

Ortonormales: para que esto ocurra, un par de vectores deben contar con un producto escalar equivalente a cero y, a la vez, ser unitarios.

Fijos: se identifica bajo este nombre a aquellos vectores que actúan como los representantes de los libres. Esto significa que no solo poseen el mismo sentido, módulo y dirección, sino también comparten el punto de origen.

Colineales: en este caso, al menos dos vectores actúan en una misma línea.

De posición: se conoce bajo este nombre a los vectores cuyo punto de origen de coordenadas se unifica con un vector de posición determinado.

Unitarios: se identifica como tal a los vectores cuyo módulo es la unidad.

Resultante: se conoce bajo este nombre a aquellos vectores que generan el mismo efecto que los componentes, en el sistema.

Equilibrante: los vectores conocidos bajo este nombre son los que cuentan con la misma dirección, así como también magnitud que el vector resultante. La diferencia entre ambos tiene que ver con el sentido, que es opuesto en 180°.